Entanglement has far reaching applications across all frontiers of modern physics. One important application that has garnered much interest is its ability to pick up signatures of quantum phase transitions and crossovers. In our work, we probed for such signatures in the zero-mode regime of a lattice-regularized massive scalar field in (1+1)-dimensional space-time. The regularized model is characterized by N (number of oscillators that make up the lattice), a (lattice spacing), and m_f (mass of the scalar field). We proceeded to study three different quantities :
-
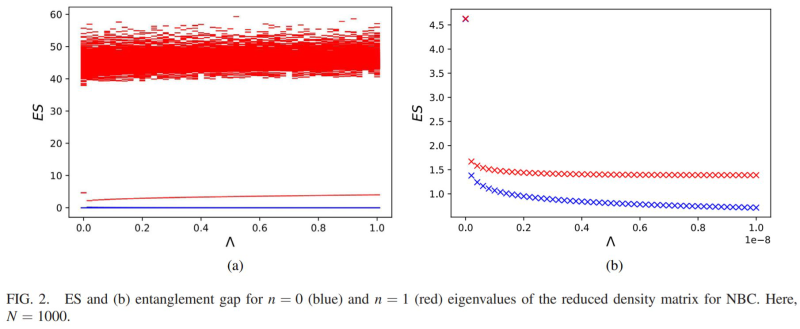
Entanglement Spectrum (ES) : Used to extract detailed information in entangled systems. For instance, in the case of fractional quantum Hall states, the low-lying levels of entanglement spectrum capture information about the edge modes that help identify topological order, as well as the CFT associated with it. The difference between the lowest two levels in the spectrum, known as the ``entanglement gap", further contains signatures of symmetry-breaking and quantum phase transitions in many-body systems. On numerically simulating this gap for the scalar field, we observed that---i) The gap closes in the presence of a zero-mode, indicating quantum criticality, and ii) The gap shows a sharp change in behavior very close to criticality, hinting at a crossover.
-
Entanglement Entropy : Standard measure of entanglement that can be derived equivalently from either the reduced density matrix or the reduced covariance matrix of an entangled system. The latter approach can give us an analytical leading order expression for entropy of the reduced state of a single oscillator subsystem. Further analysis shows that the leading order term changes drastically close to criticality, as hinted by the entanglement gap simulation.

-
Overlap Function : Used to test the fidelity of neighboring quantum states in the parameter space. Similar to entanglement entropy, the overlap function also shows a drastic change in its leading order term close to criticality. This indicates that the crossover picked up by entanglement is a fundamental property of the total wave-function of the system.

Our work showed that the leading order terms of entanglement entropy as well as the overlap function are fundamentally different on either side of am_f~ 1/N, suggesting a quantum crossover in the ground state of the regularized field. For am_f>> 1/N , entropy exhibits a slow log-log divergence, and is independent of IR cutoff as well as the boundary conditions. On decreasing the rescaled mass beyond the threshold, i.e., am_f<< 1/N , entropy switches from a slow log-log divergence to a faster log divergence. In this phase, both the system and subsystem properties develop sensitivity to the IR-cutoff (or the boundaries of the system). This is a novel phase marked by an onset of zero-mode effects, wherein the gap in the entanglement spectrum begins to close, and neighboring quantum states approach orthogonality. In the thermodynamic limit, the crossover point coincides with critical point am_f=0 . The boundary-dependent phase is therefore confined to just the critical point.